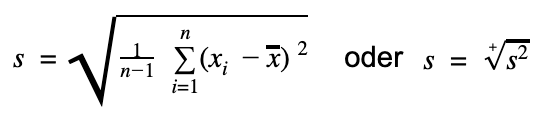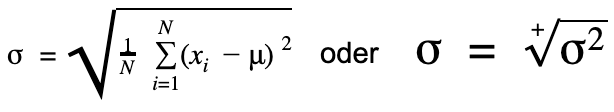Geben alle Zusammenhangsmaße Informationen über die Richtung des Zusammenhangs?
Nein, über die Richtung des Zusammenhangs informieren nur einige Zusammenhangsmaße wie der Rangkorrelationskoeffizient nach Spearman oder der Korrelationskoeffizient nach Pearson. Allerdings geben alle Zusammenhangsmaße Informationen über die Stärke eines statistischen Zusammenhangs.
Häufig gestellte Fragen: Statistik
- Wozu werden Hypothesentests benötigt?
-
Ein Hypothesentest wird dazu benötigt, Annahmen über die Welt zu überprüfen. Dazu werden Hypothesen aufgestellt, die anhand statistischer Tests überprüft werden.
- Was ist der Unterschied zwischen den Korrelationskoeffizienten nach Pearson und Spearman?
-
Wann wir welchen Korrelationskoeffizienten als Zusammenhangsmaß verwenden, hängt vom Skalenniveau unserer Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman’s Rangkorrelationskoeffizienten verwenden wir für ordinalskalierte Daten.
- Was bedeutet deskriptive Statistik?
-
In der deskriptiven Statistik geht es um das Beschreiben von Daten. Ziel ist es dabei einen Überblick über die vorliegenden Daten zu erhalten und diese zu ordnen.
- Was ist der Unterschied zwischen induktiver und deskriptiver Statistik?
-
In der deskriptiven Statistik beziehen sich alle Ergebnisse auf unseren vorliegenden Datensatz. In der induktiven Statistik schließen wir von Daten aus einer Stichprobe auf eine Grundgesamtheit.
- Was sind die wichtigsten Kennzahlen der deskriptiven Statistik?
-
In der deskriptiven Statistik werden vor allem Streuungsmaße, Lageparameter sowie Zusammenhangsmaße zum Beschreiben der Daten verwendet.
- Was ist statistische Signifikanz?
-
Statistische Signifikanz gibt an, wie wahrscheinlich es ist, dass ein Ergebnis auf Zufall basiert. Signifikanz wird i. d. R. durch einen p-Wert angegeben.
Das Signifikanzniveau, das mit dem der p-Wert verglichen wird, wird von den Forschenden selbst festgelegt und ist meistens 0.05 oder 0.01. Wenn der p-Wert kleiner ist als das gewählte Signifikanzniveau, spricht man von einem statistisch signifikanten Ergebnis.
- Was ist ein Signifikanzniveau?
-
Ein Signifikanzniveau α gibt an, was die maximale Wahrscheinlichkeit ist, mit der eine Nullhypothese fälschlicherweise abgelehnt wird. Das Signifikanzniveau legst du zu Beginn deiner statistischen Untersuchung selbst fest.
- Was ist ein Alpha-Fehler?
-
Ein Alpha-Fehler, auch Typ-1-Fehler oder false positive genannt, ist das fälschliche Ablehnen einer Nullhypothese. Es wird aus der statistischen Analyse also geschlossen, dass es einen statistisch signifikanten Zusammenhang, Effekt oder Unterschied gibt, obwohl dies eigentlich nicht der Fall ist.
Ein niedriges Signifikanzniveau erhöht die Wahrscheinlichkeit für einen Alpha-Fehler.
- Was ist der p-Wert in der Statistik?
-
Der p-Wert beschreibt die Wahrscheinlichkeit, dass die gefundene Teststatistik (oder ein extremerer Wert) in der Stichprobe vorkommt, unter der Annahme, dass die Nullhypothese wahr ist.
- Ab wann ist der p-Wert signifikant?
-
Das hängt davon ab, welches Signifikanzniveau (α) gewählt wurde. Meist ist dies 0,05.
Wenn der p-Wert kleiner ist als α, dann wird die Nullhypothese abgelehnt. - Wie kann ich den p-Wert berechnen?
-
- Der p-Wert kann am einfachsten mithilfe eines Statistikprogramms berechnet werden. Hierfür solltest du den richtigen statistischen Test durchführen.
- Alternativ gibt es im Internet Tabellen, die die p-Werte auflisten. Suche nach der richtigen Tabelle für deinen statistischen Test. Dafür benötigst du die Freiheitsgrade und die Teststatistik.
- Was ist der Unterschied zwischen Kovarianz und Korrelation?
-
Die Kovarianz ist ein nicht-standardisiertes Zusammenhangsmaß und hat daher nur eine geringe Vergleichbarkeit. Wir können aus der Kovarianz die Korrelation bestimmen. Diese ist standardisiert und lässt daher eine höhere Vergleichbarkeit zu.
- Was ist die Nullhypothese?
-
Die Nullhypothese ist das Gegenteil der Alternativhypothese und besagt, dass es keinen wirklichen Zusammenhang gibt. Mögliche Unterschiede sind demnach nur durch Zufall entstanden.
- Welchen Schritten sollte man beim Hypothesentest folgen?
-
Die vier Schritte des Hypothesentests sind: 1. Hypothesen aufstellen, 2. Daten sammeln, 3. Statistischen Test durchführen, 4. Entscheiden, ob die Nullhypothese abgelehnt oder beibehalten wird.
- Welche Arten von Hypothesentests gibt es?
-
Hypothesentests können einseitig oder beidseitig sein. Die einseitigen Tests können linksseitig oder rechtsseitig sein. Welcher Hypothesentest angebracht ist, hängt von der Forschungsfrage ab.
- Was für Fehler können beim Hypothesentest auftreten?
-
Im allgemeinen solltest du mit Verallgemeinerungen auf die gesamte Population (oder Grundgesamtheit) vorsichtig sein. Außerdem können beim Hypothesentest die Fehler 1. und 2. Art auftreten.
- Was sind Unterschiede zwischen Grundgesamtheit und Stichprobe?
-
Der Unterschied zwischen Grundgesamtheit und Stichproben besteht darin, dass die Grundgesamtheit alle Objekte umfasst, über die du Erkenntnisse gewinnen willst. Die Stichprobe ist hingegen der Teil der Grundgesamtheit, den du untersuchst, um Schlüsse zu ziehen.
- Wie kann man Daten über die Grundgesamtheit erheben?
-
Meist wird repräsentativ für die Grundgesamtheit eine Stichprobe verwendet. Manchmal ist jedoch auch eine Vollerhebung der Grundgesamtheit möglich.
- Was ist die Grundgesamtheit?
-
Die Grundgesamtheit (auch Population) ist die gesamte Anzahl an Objekten, über die du Schlüsse ziehen möchtest.
- Was genau ist eine Stichprobe?
-
Anhand bestimmter Punkte wird eine Teilmenge aus der Grundgesamtheit entnommen und untersucht. Dies nennt sich Stichprobe.
- Wie von der Stichprobe auf die Grundgesamtheit schließen?
-
Um Aussagen über die Grundgesamtheit treffen zu können, möchtest du von der Grundgesamtheit auf die Stichprobe schließen. Dazu sollte die Stichprobe repräsentativ sein. Dann wird berechnet, ob die Werte der Stichprobe von denen der Grundgesamtheit abweichen.
- Was macht eine Stichprobe repräsentativ?
-
Eine Stichprobe ist repräsentativ für die Grundgesamtheit, wenn die Merkmale der Grundgesamtheit in ihr abgebildet sind. Dabei hilft es, wenn die probabilistische Stichprobenziehung verwendet wird und der Stichprobenumfang groß ist.
- Wie kann ich den Korrelationskoeffizienten nach Pearson in Excel berechnen?
-
In Excel können wir den Korrelationskoeffizienten mit dem Befehl =KORREL() bestimmen. Gib dazu in den Klammern die Zellen an, für die du die Korrelation bestimmen möchtest. Trenne die Werte für die beiden Variablen mit einem Semikolon.
Beispiel =KORREL(B2:B30;C2:C30) - Was sagt die Standardabweichung aus?
-
Die Standardabweichung sagt aus, in welchem Umfang Werte in einem Datensatz von ihrem Durchschnittswert abweichen.
- Was ist xi bei der Standardabweichung?
-
xi in der Formel der Standardabweichung ist dein Beobachtungswert.
Beispiel Du hast 20 Personen nach dem Alter gefragt und möchtest nun die Standardabweichung des Alters in der Gruppe bestimmen. Füge für xi die einzelnen Altersangaben der Personen in die Formel der Standardabweichung ein. - Wie berechnet man die Standardabweichung?
-
Welche Formel du zur Berechnung der Standardabweichung verwendest, hängt davon ab, ob du die Daten einer Stichprobe oder einer Grundgesamtheit vorliegen hast.
Formeln zur Standardabweichung Stichprobe Grundgesamtheit Beachte Wenn du die Varianz bereits gegeben hast, kannst du die Standardabweichung auch bestimmen, indem du die Wurzel aus der Varianz ziehst.Beispiel - Wie berechnet Excel die Standardabweichung?
-
Gib in Excel =STABW.S() oder =STDEV.S() ein, um die Standardabweichung einer Stichprobe zu bestimmen. In die Klammern schreibst du dann die Zellen mit den Werten, für die du die Standardabweichung bestimmen willst.
Beispiel Deine Werte, für die du die Standardabweichung bestimmen willst, stehen in den Zellen C3 bis L3. Schreibe also in eine leere Zelle: =STABW.S(C3:L3) oder =STDEV.S(C3:L3) und du erhältst die Standardabweichung der Werte in diesen Zellen.Beachte dabei, dass es sich um die Standardabweichung einer Stichprobe handelt. Die Standardabweichung einer Grundgesamtheit kannst du in Excel mit dem Befehl =STABW.N. bestimmen.
- Was sagt die Korrelation aus?
-
Die Korrelation informiert uns über den Grad des Zusammenhangs zwischen zwei Variablen.
- Korrelationskoeffizient nach Pearson oder Spearman?
-
Verwende den Korrelationskoeffizienten nach Pearson bei metrischen Daten und den Rangkorrelationskoeffizienten nach Spearman bei ordinalen Daten, für die du eine Korrelation bestimmst.
- Bedeutet Korrelation Kausalität?
-
Nein, eine Korrelation ist zwar ein Hinweis, aber kein Beweis für einen kausalen Zusammenhang zwischen zwei Variablen.
- Was ist das gewichtete arithmetische Mittel?
-
Beim gewichteten arithmetischen Mittel werden die einzelnen Beobachtungswerte mit unterschiedlicher Gewichtung in dem Mittelwert berücksichtigt.
- Was sagt der Korrelationskoeffizient nach Pearson aus?
-
Der Korrelationskoeffizient nach Pearson gibt uns Auskunft über den Zusammenhang von zwei metrisch skalierten Variablen.
- Ab wann ist meine Korrelation hoch?
-
Von einer hohen Korrelation wird bei einem r-Wert (Korrelationskoeffizient) zwischen 0.5 und 1 oder -0.5 und -1 gesprochen.
- Was ist die Standardabweichung?
-
Die Standardabweichung ist ein Maß für die Streuung von Daten. Sie gibt die durchschnittliche Abweichung aller erhobenen Werte von ihrem Durchschnittswert an.
- Was ist der Unterschied zwischen der Pearson- und der Spearman-Korrelation?
-
Wann wir welchen Korrelationskoeffizienten verwenden, hängt vom Skalenniveau der Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman‘s Rangkorrelationskoeffizienten verwenden wir für ordinalskalierte Daten.
- Was sagt der Rangkorrelationskoeffizient aus?
-
Der Rangkorrelationskoeffizient nach Spearman gibt uns Auskunft über den Zusammenhang zwischen zwei mindestens ordinalskalierten Variablen.
Anhand des Rangkorrelationskoeffizienten können wir sagen, ob zwei Variablen zusammenhängen, und wenn ja, wie stark der Zusammenhang ist und in welche Richtung er besteht.
- Was ist Spearman’s Rho (ρ)?
-
Spearman’s Rho ist lediglich eine andere Bezeichnung für den Rangkorrelationskoeffizienten nach Spearman.
- Was ist der Unterschied zwischen der Pearson- und der Spearman-Korrelation?
-
Wann wir welchen Korrelationskoeffizienten verwenden, hängt vom Skalenniveau unserer Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman’s Rangkorrelationskkoeffizienten verwenden wir für ordinalskalierte Daten.
- Was sagt Cramers V aus?
-
Cramers V gibt uns Auskunft über den statistischen Zusammenhang zwischen zwei oder mehreren nominalskalierten Variablen.
- Was ist der Unterschied zwischen Cramers V und Chi-Quadrat?
-
Cramers V ist ein standardisiertes Zusammenhangsmaß und lässt daher Vergleiche mehrerer Koeffizienten zu. Chi-Quadrat ist nicht standardisiert und hat daher eine geringere Aussagekraft.
- Wie interpretiere ich Cramers V richtig?
-
Der Wert für Cramers V liegt zwischen 0 und 1. Dabei bedeutet 0, dass es überhaupt keinen Zusammenhang gibt, und 1, dass es einen vollständigen Zusammenhang gibt. Dabei gilt es zu beachten, dass wir anhand von Cramers V zwar Aussagen über die Stärke, nicht aber über die Richtung des Zusammenhangs treffen können.
- Wofür benutze ich Zusammenhangsmaße?
-
Zusammenhangsmaße werden verwendet, um die Stärke und ggf. die Richtung eines statistischen Zusammenhangs zwischen zwei Variablen anzugeben.
- Woher weiß ich, welches Zusammenhangsmaß ich verwenden kann?
-
Welches Zusammenhangsmaß du verwenden kannst, hängt vom Skalenniveau deiner Daten ab. Überprüfe dazu, ob du nominale, ordinale oder metrische Daten vorliegen hast.