Arithmetisches Mittel verstehen und berechnen - mit Beispielen
Das arithmetische Mittel beschreibt den statistischen Durchschnittswert. Daher wird das arithmetische Mittel häufig auch Mittelwert oder Durchschnittswert genannt.
Arithmetisches Mittel: 167.5
Zur Berechnung addieren wir alle Beobachtungsdaten und teilen dann die Summe durch die Anzahl der Daten.
Arithmetisches Mittel Rechner
Du kannst das arithmetische Mittel mithilfe unseres arithmetisches Mittel Rechners berechnen.
Das arithmetische Mittel am Beispiel erklärt
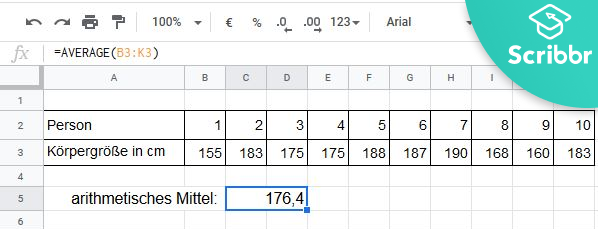
Nehmen wir an, wir haben die Körpergröße von zehn Personen gemessen und folgende Werte erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Körpergröße in cm | 155 | 183 | 175 | 175 | 188 | 187 | 190 | 168 | 160 | 183 |
| Allgemein | Beispiel | |
|---|---|---|
| 1 | Addiere zunächst alle Werte deines Datensatzes. | Wir addieren zunächst die Körpergrößen aller Personen.
155 + 183 + 175 + 175 + 188 + 187 + 190 + 168 + 160 + 183 = 1764 |
| 2 | Teile die Summe durch die Anzahl der Werte aus Schritt 1. | Insgesamt haben wir zehn Beobachtungswerte.
|
| 3 | Formuliere und interpretiere das Ergebnis. | Das arithmetische Mittel unserer Beobachtungswerte beträgt 176.4 cm. Dies sagt uns, dass die Durchschnittsgröße der zehn Personen bei 176.4 cm liegt. |
Formel zum arithmetischen Mittel
| Formel zum arithmetischen Mittel | |
|---|---|
 |
|
| x̄ | arithmetisches Mittel |
| n | Anzahl der Beobachtungen |
| x | Wert aus der Datenreihe |
Arithmetisches Mittel in Excel berechnen
In Excel können wir das arithmetische Mittel unseres Datensatzes mithilfe der Funktion MITTELWERT bestimmen.
Schreibe dazu =MITTELWERT oder =AVERAGE und gib in den Klammern die Zellen mit den Werten an, für die du das arithmetische Mittel bestimmen willst.
Da wir das arithmetische Mittel aller Körpergrößen bestimmen wollen, fügen wir B3:K3 in den Klammern ein und erhalten einen Mittelwert von 176.4 cm.
Gewichtetes arithmetisches Mittel
Eine besondere Form des arithmetischen Mittels ist das gewichtete (oder gewogene) arithmetische Mittel.
Dabei werden die einzelnen Werte mit unterschiedlicher Gewichtung in dem Mittelwert berücksichtigt.
Das gewichtete arithmetische Mittel am Beispiel erklärt:
Die Tabelle zeigt die Verteilung der Ergebnisse einer Klausur von insgesamt 24 Schülern. Nun können wir den Durchschnitt mithilfe des gewichteten arithmetischen Mittels berechnen.
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Häufigkeit | 5 | 6 | 6 | 5 | 1 | 1 |
| Allgemein | Beispiel | |
|---|---|---|
| 1 | Multipliziere die Beobachtungswerte mit deren Häufigkeit und addiere die Ergebnisse. | Wir multiplizieren die Noten mit den Häufigkeiten und addieren die Ergebnisse.
1*5 + 2*6 + 3*6 + 4*5 + 5*1 + 6*1 = 66 |
| 2 | Teile das Ergebnis aus Schritt 1 durch die Anzahl aller Beobachtungswerte. | Insgesamt haben wir 24 Beobachtungswerte.
|
| 3 | Formuliere und interpretiere das Ergebnis. | Das gewichtete arithmetische Mittel unserer Beobachtungswerte beträgt 2.75. Dies sagt uns, dass die Durchschnittsnote in der Klausur bei 2.75 liegt. |
Vergleich zu Modus und Median
Wie auch der Modus und das arithmetische Mittel gehört der Median zu den Lageparametern.
In der deskriptiven Statistik verwenden wir Lageparameter, um die zentrale Lage einer Verteilung von Daten anzugeben, also zum Beispiel den Mittelwert oder den Zentralwert.
Auch in deiner Bachelorarbeit oder Masterarbeit kannst du Lageparameter und Streuungsmaße für statistische Auswertungen verwenden.
Nehmen wir an, wir haben 20 Menschen nach ihrem Alter gefragt und folgende Werte erhalten:
| Person | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alter | 18 | 20 | 21 | 21 | 21 | 23 | 25 | 25 | 25 | 25 | 26 | 27 | 27 | 29 | 29 | 30 | 30 | 32 | 34 | 88 |
| Erklärung |
|---|
| Beim arithmetischen Mittel bestimmen wir den durchschnittlichen Wert aller Beobachtungsdaten. |
| Berechnung |
 |
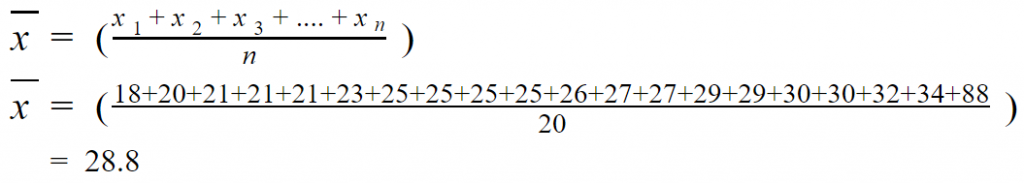| Ergebnis |
| Im Durchschnitt sind die Personen in der Gruppe 28.8 Jahre alt. |
| Erklärung |
|---|
| Beim Median bestimmen wir, welcher Wert genau in der Mitte der geordneten Reihe aller Beobachtungsdaten liegt und diese in zwei Hälften teilt. |
| Berechnung |
 |
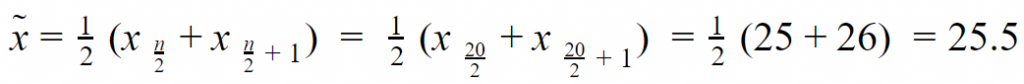| Ergebnis |
| Ein Alter von 25.5 Jahren teilt die Gruppe in zwei Hälften. |
| Erklärung | ||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beim Modus bestimmen wir, welcher Wert in unseren Beobachtungsdaten am häufigsten vorkommt. | ||||||||||||||||||||||||||
| Berechnung | ||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Ergebnis | ||||||||||||||||||||||||||
| Am häufigsten kommt ein Alter von 25 Jahren in der Gruppe vor. |
Häufig gestellte Fragen
- Was ist der Unterschied zwischen arithmetischem Mittel und Mittelwert?
-
Keiner – Mittelwert und Durchschnittswert sind lediglich andere Bezeichnungen für das arithmetische Mittel.
- Wie kann ich das arithmetische Mittel berechnen?
-
Das arithmetische Mittel kannst du in nur zwei Schritten bestimmen:
- Addiere alle Beobachtungsdaten.
- Teile die Summe durch die Anzahl der Beobachtungsdaten. Das Ergebnis ist das arithmetische Mittel deiner Beobachtungsdaten.
- Was ist das gewichtete arithmetische Mittel?
-
Beim gewichteten arithmetischen Mittel werden die einzelnen Beobachtungswerte mit unterschiedlicher Gewichtung in dem Mittelwert berücksichtigt.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Benning, V. (2023, 02. Mai). Arithmetisches Mittel verstehen und berechnen - mit Beispielen. Scribbr. Abgerufen am 11. November 2024, von https://www.scribbr.ch/statistik-ch/arithmetisches-mittel/
