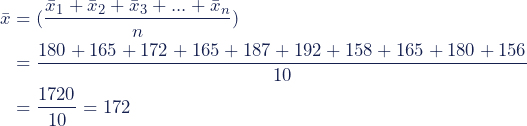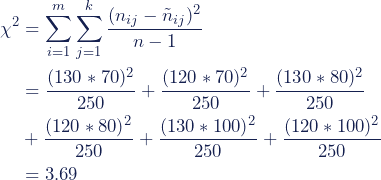Kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Kostenlose Plagiatsprüfung

Plagiate kostenlos finden

Korrektur deiner Abschlussarbeit

Fehler professionell beheben
  1. Home
  2. Wissensdatenbank
  3. Statistik
  4. Deskriptive Statistik verstehen und anwenden

Deskriptive Statistik verstehen und anwenden

Veröffentlicht am 20. August 2020 von Valerie Benning.

Ziel der deskriptiven Statistik ist es, einen Überblick über die vorliegenden Daten zu erhalten, diese zu ordnen und zusammenzufassen.

Es geht in der deskriptiven Statistik also um das Beschreiben von Daten und die Ergebnisse beziehen sich dabei immer direkt auf den vorliegenden Datensatz.

Merke
Neben der deskriptiven Statistik gibt es noch die induktive Statistik (auch Inferenzstatistik genannt). Hierbei werden Aussagen über einen Datensatz hinaus getroffen, indem von einer Stichprobe auf eine Grundgesamtheit geschlossen wird.

Kennzahlen in der deskriptiven Statistik mit Beispielen

Zum Beschreiben der Daten werden vor allem drei Kennzahlen verwendet: Streuungsmaße, Lageparameter und Zusammenhangsmaße.

Kennzahlen in der deskriptiven Statistik mit Beispielen

Nehmen wir an wir haben zehn Personen nach ihrer Körpergröße gefragt und die folgenden Antworten erhalten:

Person 1 2 3 4 5 6 7 8 9 10
Körpergröße in cm 180 165 172 165 187 192 158 165 180 156

Zur Bestimmung der Parameter wissen wir also bereits: n = 10.

Wusstest du schon, dass ...

Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?

Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.

Erfahre mehr zur Korrektur

Lageparameter

Lageparameter werden in der deskriptiven Statistik verwendet, um die zentrale Lage einer Verteilung von Daten anzugeben, also zum Beispiel den Mittelwert oder den Zentralwert.

Die wichtigsten Lageparameter sind

Arithmetisches Mittel

Das arithmetische Mittel (auch Mittelwert) beschreibt den statistischen Durchschnittswert deiner Daten.

Zur Berechnung addieren wir alle Beobachtungsdaten und teilen dann die Summe durch die Anzahl der Daten.

Berechnung:

    \begin{align*} \bar{x} &= (\frac {{\bar{x}_1} + {\bar{x}_2} + {\bar{x}_3} + ... + {\bar{x}_n}}{n}) \\ &= \frac {{180} + {165} + {172} + {165} + {187} + {192} + {158} + {165} + {180} + {156}}{10} \\ &= \frac {1720}{10} = 172 \end{align*}

Die durchschnittliche Größe der befragten Personen beträgt 172 cm.

Modus

Der Modus (auch Modalwert) ist der Wert, der in einem Datensatz am häufigsten vorkommt.

Körpergröße 156 158 165 172 180 187 192
Häufigkeit 1 1 3 1 2 1 1

Der Modus der befragten Personen liegt bei 165 cm. Diese Körpergröße kommt am häufigsten in den Beobachtungsdaten vor.

Median

Der Median (auch Zentralwert) ist der Wert, der genau in der Mitte einer Datenreihe liegt, die nach der Größe geordnet ist.

Berechnung:
geordnete Reihe: 156, 158, 165, 165, 165, 172, 180, 180, 187, 192

\tilde{x}= \frac {1}{2} (x_\frac {n}{2}+x_{\frac{n}{2} + 1})=\frac {1}{2} (x_\frac {10}{2}+x_{\frac{10}{2} + 1})=\frac {1}{2} (165 + 172)=168.5

Der Median liegt bei 168.5 cm. Diese Körpergröße liegt genau in der Mitte der geordneten Datenreihe und teilt die Gruppe in zwei Hälften.

Streuungsmaße

Streuungsmaße werden in der deskriptiven Statistik verwendet, um die Verteilung und die Streubreite von Daten anzugeben.

Zu den Streuungsmaßen zählen

Varianz

Die Varianz gibt an, wie sich deine Beobachtungswerte um den Mittelwert aller Beobachtungen verteilen.

Berechnung:

s^2 = \frac{1}{n-1}\sum ^n _{i=1}(x_i - \bar{x})^2=\frac{1}{10-1}\sum ^{10} _{i=1}(x_i - 172)^2 = 150.22

Die Varianz beträgt 150.22 (cm2).

Standardabweichung

Die Standardabweichung ist ein Maß für die Streuung von Daten. Sie gibt an, in welchem Umfang erhobene Werte vom Durchschnittswert abweichen.

Zur Berechnung ziehen wir die Wurzel aus der Varianz.

Berechnung:

s=\sqrt{s^2}=\sqrt{150.22}=12.26

Die Standardabweichung beträgt 12.26 cm, d. h., dass die Körpergrößen durchschnittlich um 12.26 cm von der Durchschnittsgröße von 172 cm abweichen.

Spannweite

Die Spannweite ist der Abstand zwischen dem kleinsten und dem größten Wert des Datensatzes.

Zur Berechnung ziehen wir das Minimum eines Datensatzes vom Maximum ab.

Berechnung:

R=x_{max}-x_{min}=192-156=36

Die Spannweite liegt bei 35 cm, d. h., dass der Abstand zwischen der kleinsten und der größten befragten Person 26 cm beträgt.

Zusammenhangsmaße

Zusammenhangsmaße geben uns Auskunft über die Stärke (und in manchen Fällen zusätzlich über die Richtung) eines statistischen Zusammenhangs zwischen zwei Variablen.

Welches Zusammenhangsmaß du verwenden kannst, hängt vom Skalenniveau deiner Daten ab.

Zu den Kennzahlen des statistischen Zusammenhangs zählen

Korrelationskoeffizent nach Pearson

Um den Zusammenhang zwischen zwei metrischen Variablen anzugeben, bestimmen wir die Kovarianz und (daraus) den Korrelationskoeffizienten.

Beispiel:
Nehmen wir an, wir haben zusätzlich zu der Körpergröße auch das Gewicht der zehn Personen erhoben. Nun wollen wir den Zusammenhang zwischen den beiden Variablen “Körpergröße” und “Gewicht” bestimmen.

Person 1 2 3 4 5 6 7 8 9 10
Körpergröße in cm 180 165 172 165 187 192 158 165 180 156
Gewicht in kg 75 60 70 65 85 90 57 58 65 53

Dazu berechnen wir zunächst die Kovarianz und erhalten ein Ergebnis von sxy= 136.44, was bedeutet, dass ein positiver Zusammenhang zwischen den beiden Variablen “Körpergröße und “Gewicht” besteht.

Im Artikel zur Kovarianz findest du eine Schritt-für-Schritt Anleitung zur Berechnung dieses Wertes.

Außerdem haben wir über die Formel der Standardabweichung folgende Werte bestimmt:

sx = 12.26 (für die Variable Körpergröße)
sy = 12.04 (für die Variable Gewicht)

Nun fügen wir die Kovarianz und die Standardabweichungen der beiden Variablen in die Formel zum Korrelationskoeffizienten ein:

r=\frac {s_{xy}}{{s_x}{s_y}}=\frac {136.44}{12.26*12.04}=0.92

Die Korrelation zwischen den beiden Variablen “Körpergröße” und “Gewicht” beträgt r = 0.92.

Rangkorrelationskoeffizient nach Spearman

Um den Zusammenhang zwischen zwei ordinalen Variablen anzugeben, bestimmen wir den Rangkorrelationskoeffizienten nach Spearman.

Beispiel:
Wir haben acht Studierende nach Ihren Abiturnoten in den Fächern Deutsch und Englisch gefragt und wollen nun den Zusammenhang zwischen den beiden Variablen bestimmen.

Person 1 2 3 4 5 6 7 8
Punkte in Deutsch 14 8 11 6 15 13 7 9
Punkte in Englisch 11 15 8 10 13 12 9 14

Dazu berechnen wir den Rangkorrelationskoeffizienten und und erhalten einen Wert von ρ = 0.19.

Im Artikel zum Rangkorrelationskoeffizienten findest du auch eine Schritt-für-Schritt Anleitung zur Berechnung dieses Wertes.

Kontingenkoeffizient

Um den Zusammenhang zwischen zwei nominalen Variablen anzugeben, können wir den Chi-Quadrat-Wert und daraus Cramers V und den Kontingenzkoeffizienten bestimmen.

Beispiel:
Wir haben 250 Personen von drei verschiedenen Studienrichtungen, nämlich Jura, Naturwissenschaften (NW) und Sozialwissenschaften (SW) befragt und wollen nun den Zusammenhang zwischen der Wahl der Studienrichtung und dem Geschlecht der Studierenden bestimmen.

Jura NW SW Summe (Zeile)
Weiblich 38 35 57 130
Männlich 32 45 43 120
Summe (Spalte) 70 80 100 250

Dazu bestimmen wir zunächst den Chi-Quadrat-Wert und wandeln diesen dann in den Kontingenzkoeffizienten um.

In unserem Beispiel haben wir ein Chi-Quadrat von χ2 = 3.69.

    \begin{align*} \chi^2 &= \sum^m _{i=1}\sum^k _{j=1}{\frac {(n_{ij} - \tilde{n}_{ij})^2}{n-1}} \\ &=\frac {(130*70)^2}{250}+\frac {(120*70)^2}{250}+\frac {(130*80)^2}{250} \\ &+\frac {(120*80)^2}{250}+\frac {(130*100)^2}{250}+\frac {(120*100)^2}{250} \\ &=3.69 \end{align*}

Nun setzen wir den Chi-Quadrat-Wert von χ2 = 3.69 in die Formel zum Kontingenzkoeffizienten nach Pearson ein:

K^P=\sqrt{\frac{\chi^2}{n+\chi^2}*\frac{M}{M-1}}=\sqrt{\frac{3.69}{250+3.69}*\frac{2}{2-1}}=0.17

Anhand des Ergebnisses von KP = 0.17 können wir ablesen, dass es einen schwachen statistischen Zusammenhang zwischen den Variablen “Geschlecht” und “Studienrichtung” gibt.

Beachte
In der Formel zum Kontingenzkoeffizienten steht M für die kleinere der beiden Anzahlen an Zeilen und Spalten. In unserem Beispiel haben wir zwei Zeilen (Geschlecht: männlich/weiblich) und drei Spalten (Studienrichtung: Jura/Naturwissenschaften/Sozialwissenschaften), also setzen wir M = 2 ein.

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Unterschied zwischen deskriptiver und induktiver Statistik

Der zentrale Unterschied besteht darin, dass wir in der deskriptiven Statistik ausschließlich Aussagen über unsere Daten treffen, während wir in der induktiven Statistik (auch Inferenzstatistik genannt) von Daten aus einer Stichprobe auf eine Grundgesamtheit schließen.

Tipp zur deskriptiven Statistik in deiner Abschlussarbeit

Im Ergebnisteil einer Bachelorarbeit oder Masterarbeit wird meist mit den deskriptiven Statistiken begonnen. So bekommen Lesende einen Überblick über die erhobenen Daten und die Stichprobe.

Im nächsten Schritt kannst du dann zu den Ergebnissen deiner statistischen Analysen und Signifikanztests übergehen.

Merke
Zur besseren Übersicht werden die Ergebnisse der deskriptiven Statistik oft in Tabellen oder Graphen dargestellt.

Beispiel zur deskriptiven Statistik im Ergebnisteil

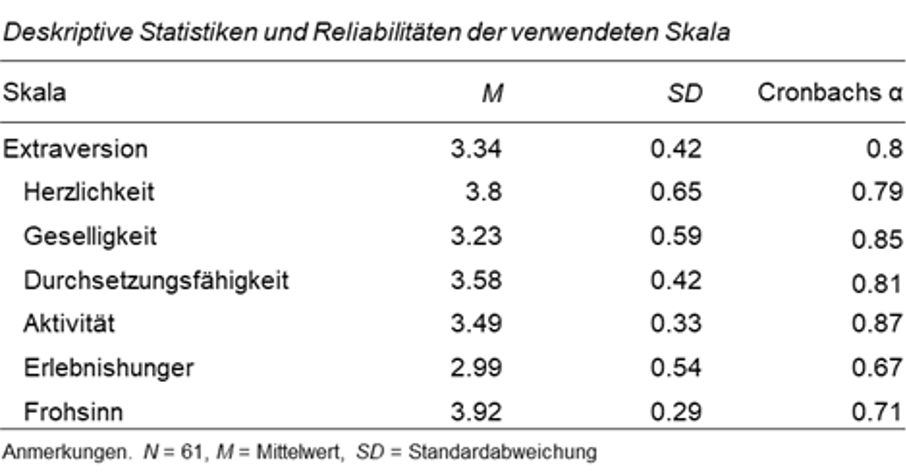
Nehmen wir an, wir haben die Variable Extraversion anhand unserer Stichprobe erhoben und stellen nun die Mittelwerte, Standardabweichungen und Reliabilitäten der einzelnen Facetten in einer Tabelle dar.

Die Tabelle zeigt dir ein Beispiel, wie du die deskriptiven Statistiken in deiner Abschlussarbeit übersichtlich darstellen kannst.
beispiel deskriptive statistik im ergebnisteil

Häufig gestellte Fragen

Was bedeutet deskriptive Statistik?

In der deskriptiven Statistik geht es um das Beschreiben von Daten. Ziel ist es dabei einen Überblick über die vorliegenden Daten zu erhalten und diese zu ordnen.

Was ist der Unterschied zwischen induktiver und deskriptiver Statistik?

In der deskriptiven Statistik beziehen sich alle Ergebnisse auf unseren vorliegenden Datensatz. In der induktiven Statistik schließen wir von Daten aus einer Stichprobe auf eine Grundgesamtheit.

Was sind die wichtigsten Kennzahlen der deskriptiven Statistik?

In der deskriptiven Statistik werden vor allem Streuungsmaße, Lageparameter sowie Zusammenhangsmaße zum Beschreiben der Daten verwendet.

Diesen Scribbr-Artikel zitieren

Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.

Benning, V. (2020, 20. August). Deskriptive Statistik verstehen und anwenden. Scribbr. Abgerufen am 11. November 2024, von https://www.scribbr.ch/statistik-ch/deskriptive-statistik/

Diesen Artikel zitieren
War dieser Artikel hilfreich?
Valerie Benning

Hi, ich bin Valerie und schreibe zur Zeit selbst meine Masterarbeit in Psychologie. Meine Erfahrungen aus dem Studium teile ich gerne, damit Studierenden statistische Themen leichter fallen.