Den p-Wert in der Statistik verstehen und interpretieren
Der p-Wert gibt an, mit welcher Wahrscheinlichkeit das gemessene Ergebnis der Stichprobe zustande gekommen sein könnte, falls die Nullhypothese stimmt.
Somit können Schlüsse darüber gezogen werden, ob gefundene Unterschiede oder Zusammenhänge zwischen Variablen durch Zufall entstanden sind oder nicht.
Eine Nullhypothese aufstellen
Die Nullhypothese besagt, dass es keinen statistischen Zusammenhang zwischen den unabhängigen und abhängigen Variablen gibt. Dies bedeutet, dass die gemessenen Zusammenhänge nur durch Zufall entstanden sind.
Als Gegensatz zur Nullhypothese wird immer eine Alternativhypothese aufgestellt.
Nullhypothese H0: Die Zufriedenheit hängt nicht damit zusammen, ob es Sommer oder Winter ist. Die Menschen sind im Sommer und im Winter gleich zufrieden.
Alternativhypothese H1: Im Sommer sind die Menschen zufriedener.
Um bestimmen zu können, ob die Nullhypothese abgelehnt werden sollte, wird nun der p-Wert benötigt.
Was genau ist der p-Wert?
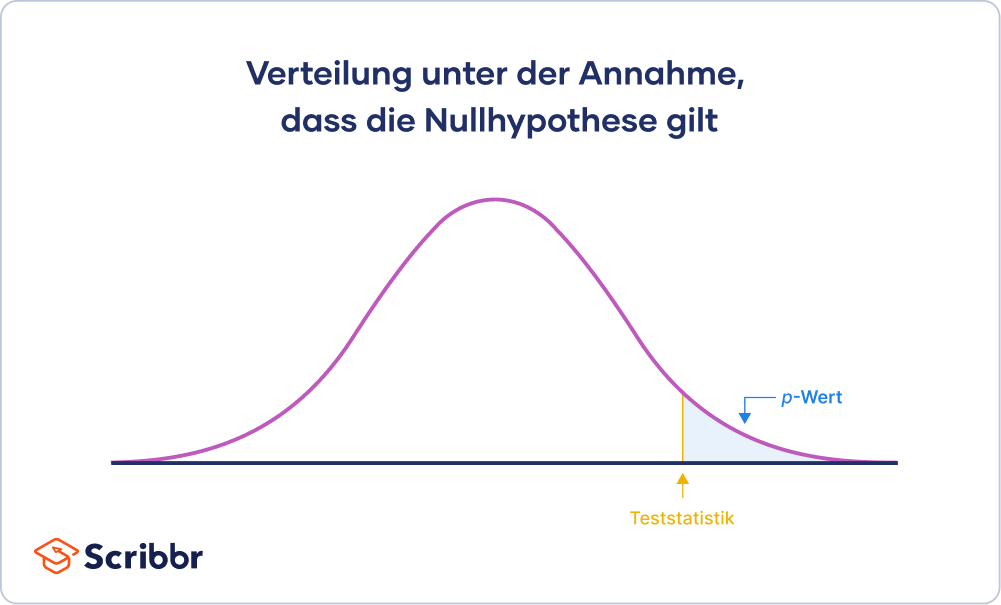
Der p-Wert gibt an, wie wahrscheinlich die Ergebnisse der Stichprobe (oder extremere Ergebnisse) sind, unter der Annahme, dass die Nullhypothese stimmt. Der p-Wert kann anhand der Teststatistik mit dem passenden statistischen Test berechnet werden.
Die Teststatistik wird aus den Daten der Stichprobe berechnet und beschreibt, ob die Verteilung der erhobenen Daten mit der Verteilung übereinstimmt, die von der Nullhypothese vorhergesagt wird.
Die gemessenen Daten werden mit dem verglichen, was wäre, wenn die Nullhypothese stimmen würde. Der p-Wert zeigt genau, wie wahrscheinlich die von der Studie gewonnene Teststatistik oder ein extremerer Wert ist, wenn die Nullhypothese wahr ist.
Ein ‚extremerer Wert‘ meint hier einen Wert, der verglichen mit der Nullhypothese noch unwahrscheinlicher ist. Es geht also um alle Werte, die in der Verteilung noch unwahrscheinlicher sind als die beobachtete Teststatistik.
Je kleiner der p-Wert, desto unwahrscheinlicher ist es, dass die beobachteten Daten unter der Nullhypothese vorkommen können.
Alternativhypothese H1: Im Sommer sind die Menschen zufriedener.
Hoher p-Wert: Der p-Wert ist hoch, wenn die Befragten in der Studie unabhängig von der Jahreszeit gleich zufrieden sind.
Dies deutet darauf hin, dass die Jahreszeit wahrscheinlich nicht entscheidend dafür ist, ob die Menschen zufrieden sind. Es gibt wahrscheinlich keinen Zusammenhang zwischen der Zufriedenheit der Befragten und der Jahreszeit.
Niedriger p-Wert: Der p-Wert ist niedrig, wenn die Befragten durchschnittlich zufriedener im Sommer sind.
Gehen wir also davon aus, dass Menschen im Sommer und im Winter gleich zufrieden sind (H0). Dann ist es sehr unwahrscheinlich, Daten wie unsere zu finden, die zeigen, dass die Menschen im Sommer viel zufriedener sind.
Unter Annahme der Nullhypothese ist es also unwahrscheinlich, die anhand der Stichprobe berechnete Teststatistik (oder extremere Werte) zu erhalten. Somit fällt der p-Wert gering aus.
Der p-Wert ist eine Wahrscheinlichkeit und kann deswegen theoretisch Werte von Null bis Eins annehmen. Liegt der p-Wert also bei 0,05, dann findet man in 5 % der Fälle eine Teststatistik, die mindestens so extrem ist wie die beobachtete, wenn die Nullhypothese wahr ist.
In der Praxis kann der p-Wert niemals Null sein, da immer eine kleine Möglichkeit besteht, dass die Ergebnisse der Studie nur durch Zufall entstanden sind.
Der p-Wert und das Signifikanzniveau
Da der p-Wert anzeigt, wie wahrscheinlich die Ergebnisse unter der Nullhypothese sind, wird er dazu verwendet, zu entscheiden, ob die Nullhypothese abgelehnt wird oder nicht.
Nun stellt sich die Frage, ab wann der p-Wert so klein ist, dass die Nullhypothese abgelehnt werden sollte. Dies wird anhand eines festgelegten Signifikanzniveaus entschieden.
Am üblichsten ist es, ein Signifikanzniveau von 0,05 zu wählen. Die Nullhypothese wird also abgelehnt, sobald die Ergebnisse der Studie zu weniger als 5 % wahrscheinlich sind, wenn die Nullhypothese stimmt.
In einigen Fällen wird sich aber auch für ein Signifikanzniveau von 0,01 oder sogar 0,001 entschieden. Dies hängt davon ab, wie sicher das Ergebnis sein sollte. Wenn beispielsweise die Nebenwirkungen eines Medikamentes gemessen werden, sollte man sich sicher sein, dass diese nicht fatal sind. Dann wird ein höheres Signifikanzniveau (also 0,01 oder 0,001) gewählt.
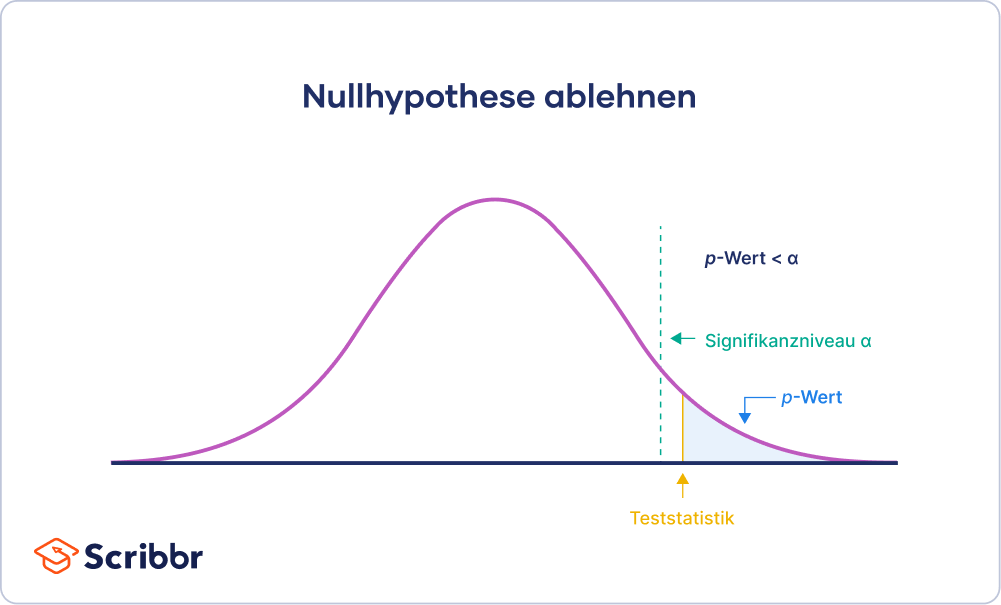
Das Signifikanzniveau wird Alpha (α) genannt. Ist der p-Wert kleiner als α, wird die Nullhypothese abgelehnt und die Alternativhypothese wird bestätigt.
Alternativhypothese H1: Im Sommer sind die Menschen zufriedener.
Das vorher festgelegte Signifikanzniveau unserer Studie liegt bei α = 0,05 und der p-Wert liegt bei 0,03.
Die Nullhypothese kann daher abgelehnt werden. Es ist unwahrscheinlich, dass die Ergebnisse nur durch Zufall entstanden sind.
Man kann also schließen, dass die Zufriedenheit von der Jahreszeit abhängt. In welcher Jahreszeit die Menschen zufriedener sind, kann man herausfinden, indem man sich die Durchschnittswerte der Zufriedenheitsskala anschaut.
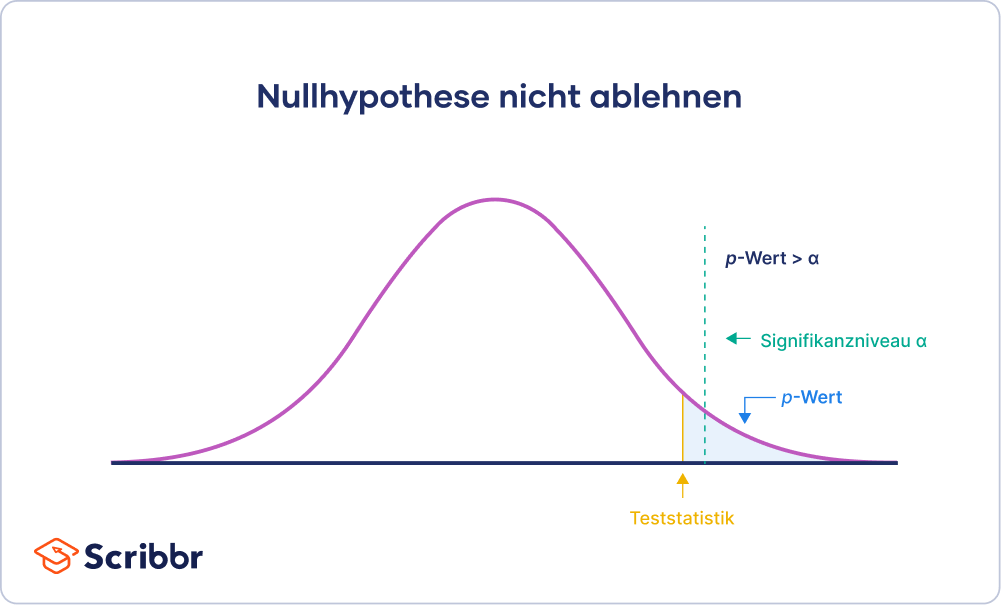
Wenn der p-Wert über α liegt und die Nullhypothese somit nicht abgelehnt wird, dann heißt das nicht, dass die Nullhypothese angenommen wird. Eine Nullhypothese kann man nur ablehnen oder beibehalten, man kann sie nicht annehmen.
Wie berechnet man den p-Wert?
Der p-Wert kann automatisch mit der gewählten Statistiksoftware berechnet werden (z. B. R, SPSS etc.).
Außerdem kann man online Tabellen finden, die den p-Wert auflisten. Man sollte sich die Tabelle für den statistischen Test anschauen, den man durchgeführt hat. Als weitere Informationen braucht man die Teststatistik und die Freiheitsgrade.
Im Allgemeinen hängt die Berechnung davon ab, welcher statistische Test verwendet wird. Dieser wiederum wird dadurch bestimmt, wie viele unabhängige- und abhängige Variablen es gibt und was für eine Art Variablen es sind.
Hier findest du eine Liste von statistischen Tests, die wir auf unserer Seite weiter erläutern.
Ganz gleich, welcher Test verwendet wird, der p-Wert beschreibt immer das Gleiche: wie wahrscheinlich es ist, die gefundenen Resultate (oder extremere) zu finden, wenn die Nullhypothese wahr ist.
Wusstest du schon, dass ...
Scribbr durchschnittlich 150 Fehler pro 1000 Wörter korrigiert?
Unsere Sprachexperten verbessern vor Abgabe deiner Abschlussarbeit den akademischen Ausdruck, die Interpunktion und sprachliche Fehler.
Wie gibt man den p-Wert an?
Die p-Werte der statistischen Tests werden normalerweise im Ergebnisteil der Arbeit genannt.
Außerdem sollten die anderen notwendigen Zahlen angegeben werden. Welche das sind, hängt vom statistischen Test ab. Bei einer Pearson-Korrelation sollte beispielsweise immer der Korrelationskoeffizient angegeben werden.
Alternativhypothese H1: Im Sommer sind die Menschen zufriedener.
Die Ergebnisse der Studie wurden anhand eines t-Tests berechnet. Die Zufriedenheit wurde einmal im Sommer und später an der gleichen Gruppe im Winter gemessen. Zu beiden Zeitpunkten wurden Fragebogen ausgefüllt. Jede Frage hatte Antwortmöglichkeiten von Eins bis Fünf, wobei Fünf am zufriedensten bedeutet.
Ergebnisse: Die erhobenen Daten wiesen eine höhere Zufriedenheit im Sommer (M = 4,43; SD = 1,14) als im Winter (M = 3,78; SD = 1,24) nach. Dieser Unterschied zwischen den Gruppen stellte sich als statistisch signifikant heraus (t(124) = 4,42, p = 0,03).
Häufig gestellte Fragen
- Was ist der p-Wert in der Statistik?
-
Der p-Wert beschreibt die Wahrscheinlichkeit, dass die gefundene Teststatistik (oder ein extremerer Wert) in der Stichprobe vorkommt, unter der Annahme, dass die Nullhypothese wahr ist.
- Ab wann ist der p-Wert signifikant?
-
Das hängt davon ab, welches Signifikanzniveau (α) gewählt wurde. Meist ist dies 0,05.
Wenn der p-Wert kleiner ist als α, dann wird die Nullhypothese abgelehnt. - Wie kann ich den p-Wert berechnen?
-
- Der p-Wert kann am einfachsten mithilfe eines Statistikprogramms berechnet werden. Hierfür solltest du den richtigen statistischen Test durchführen.
- Alternativ gibt es im Internet Tabellen, die die p-Werte auflisten. Suche nach der richtigen Tabelle für deinen statistischen Test. Dafür benötigst du die Freiheitsgrade und die Teststatistik.
Diesen Scribbr-Artikel zitieren
Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.
Hasselbusch, L. (2022, 03. März). Den p-Wert in der Statistik verstehen und interpretieren. Scribbr. Abgerufen am 16. Dezember 2024, von https://www.scribbr.ch/statistik-ch/p-wert/
