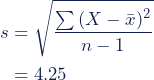Den Standardfehler des Mittelwertes verstehen und berechnen

Der Standardfehler des Mittelwertes gibt an, wie sehr der Mittelwert einer Stichprobe vom tatsächlichen Mittelwert in der Grundgesamtheit abweicht.

Der Standardfehler wird auch Stichprobenfehler oder SEM genannt. Dies ist die Abkürzung der englischen Bezeichnung ‚standard error of themean‘.

Den Standardfehler solltest du bei der Interpretation der Ergebnisse in deiner Bachelorarbeit oder Masterarbeit bedenken.

Der Standardfehler des Mittelwertes am Beispiel erklärt

Nehmen wir an, wir haben die Körpergröße von zehn Kindern im Alter von elf Jahren gemessen. Wir haben also eine Stichprobe aus allen Elfjährigen in Deutschland gezogen.

Der Mittelwert unserer Stichprobe beträgt 151.5 cm. Diesen Wert haben wir erhalten, indem wir alle Körpergrößen addiert und das Ergebnis dann durch die Gesamtanzahl 10 geteilt haben.

Würden wir nun eine neue Stichprobe aus der Grundgesamtheit (= allen Elfjährigen in Deutschland) ziehen, so könnte der Mittelwert der zweiten Stichprobe von unserem Mittelwert von 151.5 cm abweichen.

Wie weit unser Stichprobenmittelwert vom Mittelwert der Grundgesamtheit durchschnittlich abweicht, können wir mit dem Standardfehler bestimmen.

Was ist dein Score?

Erfahre binnen 10 Minuten, ob du ungewollt ein Plagiat erzeugt hast.

• 70+ Milliarden Internetquellen
• 69+ Millionen Publikationen
• Gesicherter Datenschutz

Zur Plagiatsprüfung

Den Standardfehler des Mittelwertes berechnen und interpretieren

Zur Bestimmung des Standardfehlers gibt es zwei Formeln. Welche der beiden du verwenden kannst, hängt davon ab, ob du den Mittelwert und die Standardabweichung der Grundgesamtheit gegeben hast oder nicht.

A. Mittelwert und Standardabweichung der Grundgesamtheit sind gegeben

Wenn wir den Mittelwert und die Standardabweichung der Grundgesamtheit gegeben haben, dann können wir diese in die folgende Formel einfügen und so den Standardfehler des Mittelwerts berechnen.

Formel zum Standardfehler des Mittelwertes
	Standardfehler des Mittelwertes
	Standardabweichung der Grundgesamtheit
n	Stichprobengröße

B. Mittelwert und Standardabweichung der Grundgesamtheit sind nicht gegeben

Meist sind Mittelwert und Standardabweichung der Grundgesamtheit unbekannt.

Dann verwenden wir die Standardabweichung der Stichprobe und können damit den Standardfehler schätzen.

Formel zur Schätzung des Standardfehlers
	(geschätzter) Standardfehler des Mittelwertes
	Standardabweichung der Stichprobe
n	Stichprobengröße

In 3 Schritten den Standardfehler des Mittelwertes bestimmen und interpretieren

Da wir nicht wissen, wie groß alle Elfjährigen in Deutschland durchschnittlich sind und eine Bestimmung des Mittelwertes sehr aufwendig wäre, berechnen wir den Mittelwert unserer Stichprobe und schätzen daraus den Standardfehler.

	Allgemein	Beispiel
1	Vorbereitung: Zur Bestimmung des Standardfehlers benötigen wir die Standardabweichung der Stichprobe (s) und die Gesamtanzahl (n).	Standardabweichung:     Gesamtzahl: Da wir zehn Personen befragt haben, beträgt n = 10.
2	Füge deine Werte in die Formel ein: Du berechnest die Wurzel aus n und teilst dann die Standardabweichung durch das Ergebnis.	Der Standardfehler des Mittelwertes beträgt 1.34 cm.
3	Interpretation des Ergebnisses: Der Standardfehler sagt aus, wie weit der Mittelwert der Stichprobe vom tatsächlichen Mittelwert durchschnittlich abweicht.	Ein Standardfehler von 1.34 cm bedeutet, dass die Mittelwerte unserer Stichproben durchschnittlich um 1.34 cm von der eigentlichen Durchschnittsgröße aller Elfjährigen abweichen. Da wir den Mittelwert der Stichprobe verwendet haben, handelt es sich dabei um eine Schätzung des Standardfehlers.

Unterschied von Standardfehler und Standardabweichung

Sowohl der Standardfehler als auch die Standardabweichung befassen sich mit dem Mittelwert einer Stichprobe.

Dabei gibt der Standardfehler Auskunft über die mittlere Abweichung des Mittelwerts einer Stichprobe vom tatsächlichen Mittelwert der Grundgesamtheit.

Die Standardabweichung sagt uns, wie sehr sich die einzelnen Werte der Stichprobe um ihren Mittelwert streuen.

Den Standardfehler in Excel berechnen

In Excel gibt es keine direkte Formel zur Bestimmung des Standardfehlers, daher geben wir die Formel selbst ein.

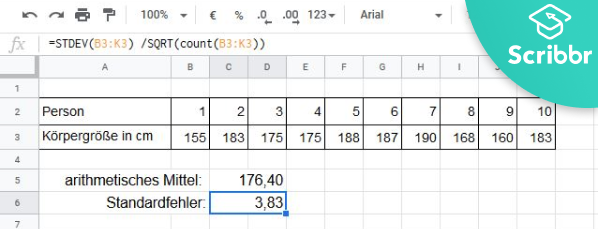
Schreibe dazu =STDEV(“ ”) /SQRT(count(“ ”)) und gib in den Klammern jeweils die Zellen mit den Werten an, für die du den Standardfehler bestimmen willst.

Da wir den Standardfehler für den Mittelwert aller Körpergrößen bestimmen wollen, fügen wir B3:K3 in den Klammern ein und erhalten einen Mittelwert von 176.4 cm und einen Standardfehler von 3.83 cm.

Häufig gestellte Fragen

Was sagt mir der Standardfehler des Mittelwertes?

Der Standardfehler des Mittelwertes gibt Auskunft über die mittlere Abweichung des Mittelwerts einer Stichprobe vom tatsächlichen Mittelwert der Grundgesamtheit.

Was bedeutet SEM?

SEM ist die Abkürzung für ‚standard error of the mean‘. Dies ist die englische Bezeichnung für den Standardfehler des Mittelwertes. Eine weitere Bezeichnung für den Standardfehler ist Stichprobenfehler.

Wie kann ich den Standardfehler berechnen?

Wie du den Standardfehler des Mittelwertes berechnen kannst, hängt von deinen Daten ab. Hast du die Standardabweichung der Grundgesamtheit gegeben, dann teile diese durch √n, also die Wurzel aus deiner Stichprobengröße.

Hast du die Standardabweichung der Grundgesamtheit nicht gegeben, dann kannst du die Standardabweichung der Stichprobe durch √n teilen und somit den Standardfehler schätzen.