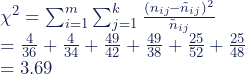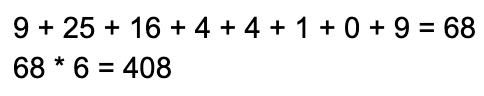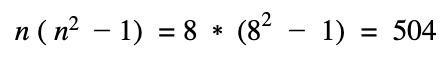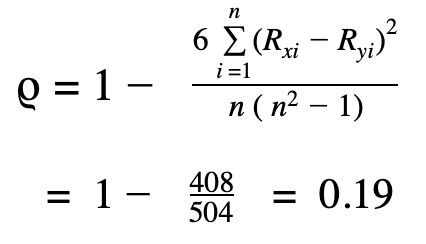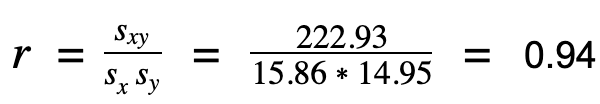Kostenlose Rechtschreibprüfung

Fehler kostenlos beheben

Kostenlose Plagiatsprüfung

Plagiate kostenlos finden

Korrektur deiner Abschlussarbeit

Fehler professionell beheben
  1. Home
  2. Wissensdatenbank
  3. Statistik
  4. Zusammenhangsmaße verstehen und bestimmen

Zusammenhangsmaße verstehen und anwenden + Beispiele

Veröffentlicht am 13. August 2020 von Valerie Benning.

Zusammenhangsmaße werden verwendet, um die Stärke eines statistischen Zusammenhangs zwischen zwei Variablen anzugeben.

Einige Zusammenhangsmaße geben darüber hinaus auch Auskunft über die Richtung des Zusammenhangs.

Welches Zusammenhangsmaß du verwenden kannst, hängt vom Skalenniveau deiner Daten ab.

Beispiel
Wir wollen den Zusammenhang zwischen der Entfernung zwischen Wohn- und Arbeitsort und der Dauer des Arbeitsweges bestimmen. Wir haben also metrische Daten vorliegen und bestimmen daher als Zusammenhangsmaß den Korrelationskoeffizienten nach Pearson.

Zusammenhangsmaße richtig anwenden

Die folgende Übersicht zeigt dir, bei welchem Skalenniveau du die verschiedenen Zusammenhangsmaße verwenden kannst und welche Formel du zur Bestimmung des Zusammenhangs benötigst.

Was ist dein Score?

Erfahre binnen 10 Minuten, ob du ungewollt ein Plagiat erzeugt hast.

  • 70+ Milliarden Internetquellen
  • 69+ Millionen Publikationen
  • Gesicherter Datenschutz

Zur Plagiatsprüfung

Nominale Daten

Bei nominalen Daten können wir den Chi-Quadrat-Wert und daraus Cramers V und den Kontingenzkoeffizienten bestimmen, um den Zusammenhang zwischen zwei Variablen anzugeben.

Chi-Quadrat

\chi^2 = \sum^m _{i=1}\sum^k _{j=1}{\frac {(n_{ij} - \tilde{n}_{ij})^2}{\tilde{n}_{ij}}}
\chi^2 Chi-Quadrat
m Gesamtanzahl der Zeilen
k Gesamtanzahl der Spalten
n_{ij} absolute Häufigkeit der Merkmalskombination in i-Zeile und j-Spalte (beobachteter Wert)
\tilde{n}_{ij} erwarteter Wert der absoluten Häufigkeit der Merkmalskombination in i-Zeile und j-Spalte

Die Formel vereinfacht in Worten:

\chi^2 = \sum{\frac {(beobachteter - erwarteter\,Wert)^2}{erwarteter\,Wert}}

Cramer‘s V

V = \sqrt{\dfrac{{x^2}}{n * (M-1)}}
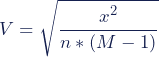V Cramers V
\chi^2 Chi-Quadrat
n Gesamtanzahl (der Stichprobe)
M M = min\,(k,m)

die kleinere der beiden Zahlen für die Zeilenanzahl (m) und die Spaltenanzahl (k) in der Kreuztabelle

Kontingenzkoeffizient

K^P=\sqrt{\frac{\chi^2}{n+\chi^2}*\frac{M}{M-1}}
K^P Kontingenzkoeffizient nach Pearson
\chi^2 Chi-Quadrat
n Gesamtanzahl (der Stichprobe)
M M = min\,(k,m)

die kleinere der beiden Zahlen für die Zeilenanzahl (m) und die Spaltenanzahl (k)

Beispiel nominales Skalenniveau

Wir wollen den Zusammenhang zwischen der Wahl der Studienrichtung und dem Geschlecht der Studierenden bestimmen. Dazu haben wir 250 Personen von drei verschiedenen Studienrichtungen, nämlich Jura, Naturwissenschaften (NW) und Sozialwissenschaften (SW) befragt und folgende Antworten erhalten:

Jura NW SW Summe (Zeile)
Weiblich 38 35 57 130
Männlich 32 45 43 120
Summe (Spalte) 70 80 100 250

Zunächst bestimmen wir den Chi-Quadrat-Wert und wandeln diesen dann in den Kontingenzkoeffizienten um.

In unserem Beispiel haben wir ein Chi-Quadrat von χ2 = 3.69.
\chi^2= \sum^m _{i=1}\sum^k _{j=1}{\frac {(n_{ij} - \tilde{n}_{ij})^2}{\tilde{n}_{ij}}} \\ = \frac {4}{36}+\frac {4}{34}+\frac {49}{42}+\frac {49}{38}+\frac {25}{52}+\frac {25}{48} \\ = 3.69
Dann setzen wir den Chi-Quadrat-Wert in die Formel für den Kontingenzkoeffizienten nach Pearson ein.

In der Formel steht M für die kleinere der beiden Anzahlen an Zeilen und Spalten. In unserem Beispiel haben wir zwei Zeilen (Geschlecht: männlich/weiblich) und drei Spalten (Studienrichtung: Jura/Naturwissenschaften/Sozialwissenschaften), also setzen wir M = 2 ein.

K^P=\sqrt{\frac{\chi^2}{n+\chi^2}*\frac{M}{M-1}}=\sqrt{\frac{3.69}{250+3.69}*\frac{2}{2-1}}=0.17

Ordinale Daten

Bei ordinalen Daten bestimmen wir den Rangkorrelationskoeffizienten nach Spearman, um den Zusammenhang zwischen zwei Variablen anzugeben.

\varrho=1-\frac{6\sum^n_{i=1} (R_{xi} - R_{yi})^2}{n(n^2-1)}
\varrho oder r_{sp} Rangkorrelationskoeffizient
R_{xi} Rang für Fall i in der geordneten Datenreihe für Variable 1
R_{yi} Rang für Fall i in der geordneten Datenreihe für Variable 2
n Gesamtanzahl der Fälle

Beispiel ordinales Skalenniveau

Wir haben acht Studierende nach ihren Abiturnoten in den Fächern Deutsch und Englisch gefragt und wollen nun den Zusammenhang zwischen den beiden Variablen bestimmen.

Person 1 2 3 4 5 6 7 8
Punkte in Deutsch 14 8 11 6 15 13 7 9
Punkte in Englisch 11 15 8 10 13 12 9 14

Dazu berechnen wir den Rangkorrelationskoeffizienten in fünf Schritten.

  1. Wir vergeben jeweils die Ränge 1–8 für die Punkte in den Fächern Deutsch und Englisch.
Person Punkte in Deutsch Rang Punkte in Englisch Rang
1 14 2 11 5
2 8 6 15 1
3 11 4 8 8
4 6 8 10 6
5 15 1 13 3
6 13 3 12 4
7 7 7 9 7
8 9 5 14 2
  1. Wir berechnen für jeden Fall einzeln die Differenz zwischen den Rängen der Noten. Anschließend quadrieren wir das Ergebnis.
Person R_{xi}-R_{yi} (R_{xi}-R_{yi})^2
1 2 – 5 = – 3 (-3)2 = 9
2 6 – 1 = 5 52 = 25
3 4 – 8 = – 4 (-4)2 = 16
4 8 – 6 = 2 22 = 4
5 1 – 3 = – 2 (-2)2 = 4
6 3 – 4 = – 1 (-1)2 = 1
7 7 – 7 = 0 02 = 0
8 5 – 2 = 3 32 = 9
  1. Wir addieren die Ergebnisse aus Schritt 2 und multiplizieren die Summe mit 6.

zusammenhangsmasse-rangkorrelationskoeffizient-berechnen-scribbr

  1. Wir setzen die Gesamtanzahl der untersuchten Fälle (n = 8) in zusammenhangsmasse-rangkorrelationskoeffizient-berechnen-formel-zum-einsetzen-scribbr ein.

zusammenhangsmasse-rangkorrelationskoeffizient-einsetzen-beispiel-scribbr

  1. Wir setzen alle Ergebnisse aus den Schritten 1–4 in die Formel ein:

zusammenhangsmasse-spearmans-rho-berechnen-scribbr
Als Ergebnis erhalten wir ρ = 0.19. Daraus können wir ablesen, dass es einen positiven Zusammenhang zwischen den Punktzahlen in den Fächern Deutsch und Englisch gibt, dieser allerdings nicht sehr stark ist.

Metrische Daten

Bei metrischen Daten können wir die Kovarianz und (daraus) den Korrelationskoeffizienten bestimmen, um den Zusammenhang zwischen zwei Variablen anzugeben.

Kovarianz

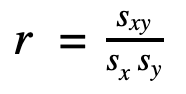korrelation-formel-scribbr
sxy Kovarianz der Variablen x und y
sx Standardabweichung der Variable x
sy Standardabweichung der Variable y
r Korrelationskoeffizient (nach Bravais)

Korrelationskoeffizient nach Pearson (r)

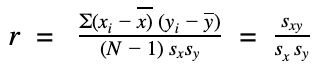formel-pearsons-r-scribbr
r Korrelationskoeffizient
xi Beobachtungswerte der Variable x
yi Beobachtungswerte der Variable y
x-bar-scribbr Arithmetisches Mittel aller Werte von x
y-bar-scribbr Arithmetisches Mittel aller Werte von y
N Gesamtanzahl
sxy Kovarianz der Variablen x und y
sx Standardabweichung der Variable x
sy Standardabweichung der Variable y

Beispiel metrisches Skalenniveau

Wir haben acht Personen nach der Entfernung zwischen ihrem Wohn- und Arbeitsort und der Dauer ihres Arbeitsweges gefragt und wollen nun den Zusammenhang zwischen den beiden Variablen bestimmen.

Person 1 2 3 4 5 6 7 8
Entfernung Wohnort – Arbeitsplatz in km 18 2 42 14 22 35 45 8
Dauer des Arbeitsweges in min 22 10 53 30 25 36 45 13

Dazu berechnen wir zunächst die Kovarianz und erhalten ein Ergebnis von sxy = 222.93, was bedeutet, dass ein positiver Zusammenhang zwischen den beiden Variablen „Entfernung” und „Dauer” besteht.

Im Artikel zur Kovarianz findest du eine Schritt-für-Schritt-Anleitung zur Berechnung dieses Wertes.

Außerdem haben wir über die Formel der Standardabweichung folgende Werte bestimmt:

sx = 15.86
sy = 14.95

Um die Stärke des Zusammenhangs mit anderen Zusammenhangsmaßen vergleichen zu können, berechnen wir aus der Kovarianz den Korrelationskoeffizienten:

zusammenhangsmasse-korrelationskoeffizient-berechnen-scribbr

Die Korrelation zwischen den beiden Variablen „Entfernung” und „Dauer” beträgt r = 0.94.

Möchtest du eine fehlerfreie Arbeit abgeben?

Mit einem Lektorat helfen wir dir, deine Abschlussarbeit zu perfektionieren.

Neugierig? Bewege den Regler von links nach rechts!

Zu deiner Korrektur

Übersicht Zusammenhangsmaße

Zum Abschluss haben wir noch einmal in der Übersicht zusammengefasst, welche Zusammenhangsmaße zu welchem Skalenniveau gehören:

Nominale Daten

Wir bestimmen den Chi-Quadrat-Wert und daraus Cramers V und den Kontingenzkoeffizienten.

Ordinale Daten

Wir bestimmen den Rangkorrelationskoeffizienten nach Spearman.

Metrische Daten

Wir bestimmen die Kovarianz und (daraus) den Korrelationskoeffizienten.

Häufig gestellte Fragen

Wofür benutze ich Zusammenhangsmaße?

Zusammenhangsmaße werden verwendet, um die Stärke und ggf. die Richtung eines statistischen Zusammenhangs zwischen zwei Variablen anzugeben.

Geben alle Zusammenhangsmaße Informationen über die Richtung des Zusammenhangs?

Nein, über die Richtung des Zusammenhangs informieren nur einige Zusammenhangsmaße wie der Rangkorrelationskoeffizient nach Spearman oder der Korrelationskoeffizient nach Pearson. Allerdings geben alle Zusammenhangsmaße Informationen über die Stärke eines statistischen Zusammenhangs.

Woher weiß ich, welches Zusammenhangsmaß ich verwenden kann?

Welches Zusammenhangsmaß du verwenden kannst, hängt vom Skalenniveau deiner Daten ab. Überprüfe dazu, ob du nominale, ordinale oder metrische Daten vorliegen hast.

Was ist der Was ist der Unterschied zwischen Kovarianz und Korrelation?

Die Kovarianz ist ein nicht-standardisiertes Zusammenhangsmaß und hat daher nur eine geringe Vergleichbarkeit. Wir können aus der Kovarianz die Korrelation bestimmen. Diese ist standardisiert und lässt daher eine höhere Vergleichbarkeit zu.

Was ist der Unterschied zwischen den Korrelationskoeffizienten nach Pearson und Spearman?

Wann wir welchen Korrelationskoeffizienten als Zusammenhangsmaß verwenden, hängt vom Skalenniveau unserer Daten ab. Um die Korrelation nach Pearson zu berechnen, benötigen wir metrische Daten. Spearman’s Rangkorrelationskoeffizienten verwenden wir für ordinalskalierte Daten.

Diesen Scribbr-Artikel zitieren

Wenn du diese Quelle zitieren möchtest, kannst du die Quellenangabe kopieren und einfügen oder auf die Schaltfläche „Diesen Artikel zitieren“ klicken, um die Quellenangabe automatisch zu unserem kostenlosen Zitier-Generator hinzuzufügen.

Benning, V. (2020, 13. August). Zusammenhangsmaße verstehen und anwenden + Beispiele. Scribbr. Abgerufen am 16. Dezember 2024, von https://www.scribbr.ch/statistik-ch/zusammenhangsmasse/

Diesen Artikel zitieren
War dieser Artikel hilfreich?
Valerie Benning

Hi, ich bin Valerie und schreibe zur Zeit selbst meine Masterarbeit in Psychologie. Meine Erfahrungen aus dem Studium teile ich gerne, damit Studierenden statistische Themen leichter fallen.